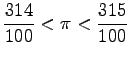- [Student ] What is
 really?
really?
- [Teacher ] Well, as usual, I will answer your question with questions
and you will discover the meaning of
 . What is blue?
. What is blue?
- [Student ] Huh?
- [Teacher ] Tell me, what is ``blue'' really?
- [Student ] Well, it is a color.
(Teacher nods and raises eyebrows and waits.)
- [Student ] Well, the sky is blue.
- [Teacher ] The sky is blue? Does that mean I can use the words interchangeably? The blue is full of birds...?
- [Student ] Aw, come on! Okay, this book is blue, that door is blue...
- [Teacher ] Right. You are giving me examples of blue things. Have you said what blue really is?
- [Student ] Well, no, not precisely...
- [Teacher ] That's because the notion of ``blue'' is abstract.
- [Student ] Uh, huh, like red.
- [Teacher ] Yes, or two, think about two, what does it really mean?
(Student smiles and holds up two fingers)
- [Teacher ] Yes, that's an example of two things, two fingers, just as the chair and door are examples of blue things.
- [Student ] So what is
 ?
?
- [Teacher ] Let me give you some examples of
 things and you'll be able to see the pattern... Imagine you have some model trains and a whole lot of little model train tracks. You place a big circle of track on the floor for one train to go around and you put a straight piece through the center for a second train to travel. Do you see what I mean?
things and you'll be able to see the pattern... Imagine you have some model trains and a whole lot of little model train tracks. You place a big circle of track on the floor for one train to go around and you put a straight piece through the center for a second train to travel. Do you see what I mean?
- [Student ] You mean like this.
( Student sketches a circle and diameter on the desktop)
- [Teacher ] Exactly. Now, you let one train go across the center and another go around the circle. The little trains are going the same speed. You start them both at the same time. The train on the straight track takes about a minute to get across from one side to the other. The train on the circular track will take
 minutes to go all the way around the circle.
minutes to go all the way around the circle.
- [Student ] Huh? It takes
 minutes?
minutes?
- [Teacher ] Yes, let me give you another example of a
 thing, it may take a few to see the pattern of what
thing, it may take a few to see the pattern of what  things are.
things are.
- [Student ] Okay. Shoot.
- [Teacher ] Suppose there is a sticky soda ring on a table.
- [Student ] A ``sticky soda ring ?''
- [Teacher ] Yes, the kind left by a leaky can of Pepsi. Suppose two ants are crawling around on the table. One crawls around the soda ring and one ant walks directly across the center of the ring from one side to the other. The ant crawling straight across takes 100 tiny ant steps. The ant crawling around the sticky circle takes 314 steps and it almost finishes the circle. The 315
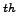 step brings him well across the line where he started. The ant on the circle took
step brings him well across the line where he started. The ant on the circle took  times as many steps as the ant travelling across the center.
times as many steps as the ant travelling across the center.
- [Student ] Okay, 100 across the middle versus 315 around the outside.
- [Teacher ] Yes, going around the outside takes
 times as many steps and the 315
times as many steps and the 315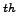 step more than completes the trip around the circle. Now I want you to write a short paragraph describing something
step more than completes the trip around the circle. Now I want you to write a short paragraph describing something  .
.
- [Student ] What?!?
- [Teacher ] Using the two examples I gave you as a guide, make up a
 story of your own.
story of your own.
- [Student ]Yeah, okay...
(a few minutes later... )
- [Teacher ] Here's a way of testing the
 -ness of your story. The examples I gave involve a comparison between what are called the diameter (the length of a line straight across a circle through its center) and the circumference (the length around the edge) of a circle. The mathematical
definition of
-ness of your story. The examples I gave involve a comparison between what are called the diameter (the length of a line straight across a circle through its center) and the circumference (the length around the edge) of a circle. The mathematical
definition of  is the ratio of the two:
is the ratio of the two:
- [Student ] No matter what?
- [Teacher ] Yes, this ratio is always
 no matter how large or small the circle. There is a fundamental quality to circular things and it is described by this number
no matter how large or small the circle. There is a fundamental quality to circular things and it is described by this number  just as there is a fundamental quality, however abstract, of blueness for blue things and two-ness for two things.
just as there is a fundamental quality, however abstract, of blueness for blue things and two-ness for two things.
- [Student ] Okay. So, maybe my example is...okay: the amount of pennies around and across a circle. (Pause) So is
 a number?
a number?
- [Teacher ] Yes, it is a number derived from the definition I gave. Let's look at the approximate size of
 as a number. Can you guess it from the ant example? Use the mathematical definition.
as a number. Can you guess it from the ant example? Use the mathematical definition.
- [Student ] You mean like circumference over diameter?
- [Teacher ] Yes, exactly.
- [Student ] Well, then, the ant example would be 315 over 100 so
 must be 3.15.
must be 3.15.
- [Teacher ] Why did you use 315?
- [Student ] YOU said that the ant wasn't all the way around in 314 steps, but was all the way in 315 steps, so it must be 315!
- [Teacher ] True, but what if the ant was, oh, in mid-stride when he crossed the starting point? I only said that he had passed the place he started in the 315
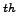 step...
step...
- [Student ] Oh. Well...then it is something between 314 and 315?
- [Teacher ] What is between 314 and 315?
- [Student ]
 !
!
- [Teacher ] Be careful to remember the definition of
 , it is a ratio.
, it is a ratio.
- [Student ] Oh, yeah, I mean that
 is somewhere between 314 over 100 and 315 over 100.
is somewhere between 314 over 100 and 315 over 100.
- [Teacher ] Go ahead and write that down.
- [Student ] Write it down?
- [Teacher ] Yes, write it in a mathematical sentence, using less-than symbols.
- [Student: ] You mean like this?
- [Teacher ] Good. Now write it using decimal fractions.
- [Student ] Okay, so
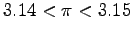 .
.
- [Teacher ] Right. So what is
 anyway?
anyway?
- [Student ] Its a number between 3.14 and 3.15...
- [Teacher ](smiling) ...and what does
 mean?
mean?
- [Student ](smiling) It is the ratio of circumference to diameter for any circle there is in the world.
- [Teacher ] Exactly.